[ethereum] 개인키와 공개키 그리고 트랜잭션 서명
이번 포스트에서는 개인키와 공개키가 생성되는 과정과 트랜잭션을 서명하고 검증하는 방법을 다룹니다.
또한 트랜잭션을 서명하는 과정에서 Simple Replay Attack Protection을 위해 EIP-155를 적용합니다.
본론을 들어가기 앞서서 선행되어야 하는 개념이 있습니다. 바로 ECC인 타원곡선 암호화와 modular(나머지) 연산 입니다.
● ECC(Elliptic Curve Cryptography)
ECC는 타원 곡선 암호화라고 불리면 공개키 암호화 방식입니다.
· 정의
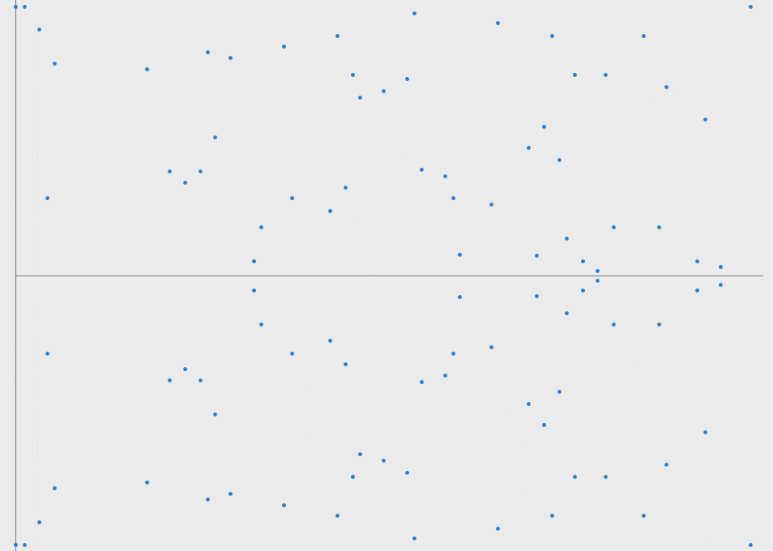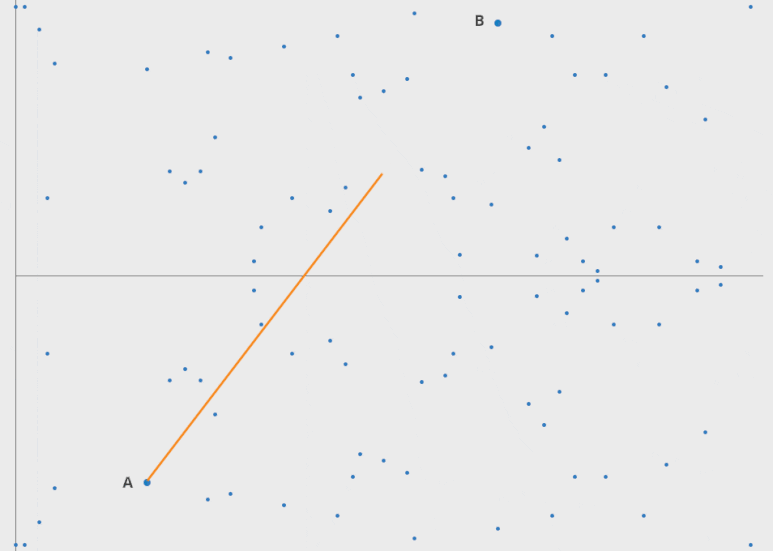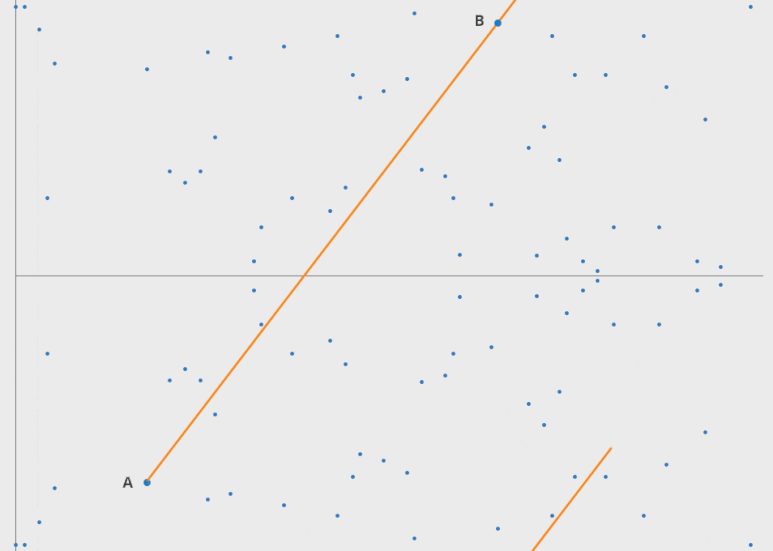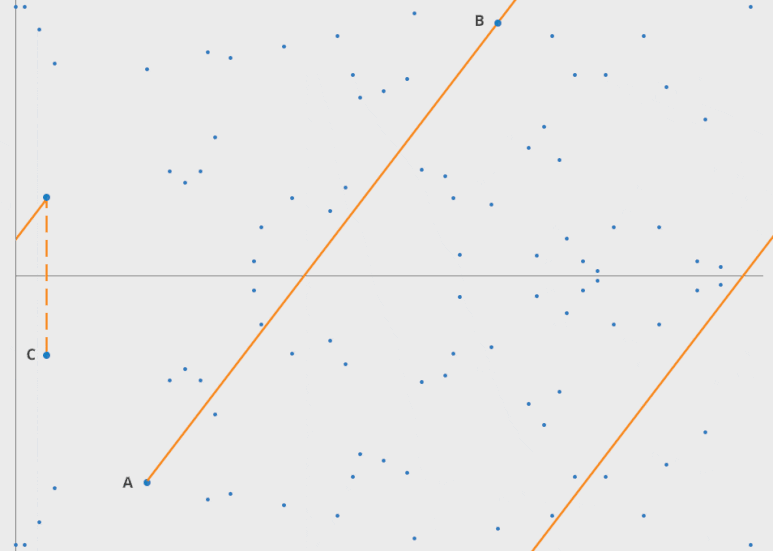
타원곡선은 다음과 같이 정의합니다.

타원곡선 함수
타원곡선은 x을 중심으로 대칭입니다. 그 이유는 y가 제곱 형태를띄기때문 입니다.
해당 링크에서 a와 b값에 따라 그래프가 어떤 모습을 보여주는지 확인할 수 있습니다.
· 연산
타원 곡선 암호화인 ECC를 이해하기 위해선 타원 곡선 함수에서 덧셈 연산을 이해해야 합니다.
타원곡선 상에 다음과 같이 2개의 점을 점 P, 점 Q라고 정의합니다.
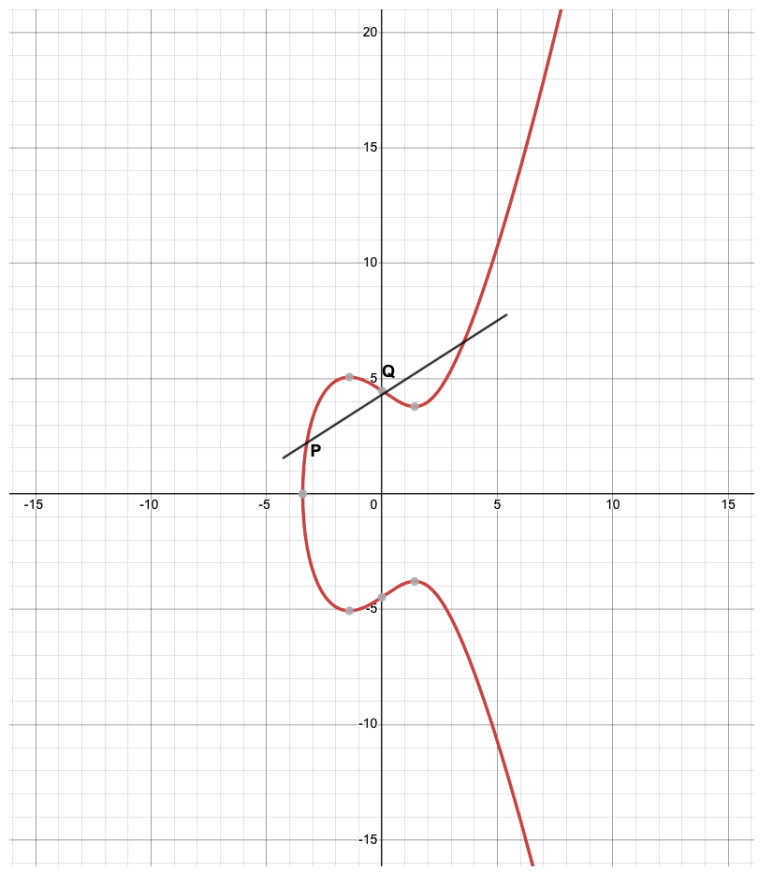
점 P와 Q를 지나는 직선과 타원곡선이 만나는 교점을 -R이라고 합니다.
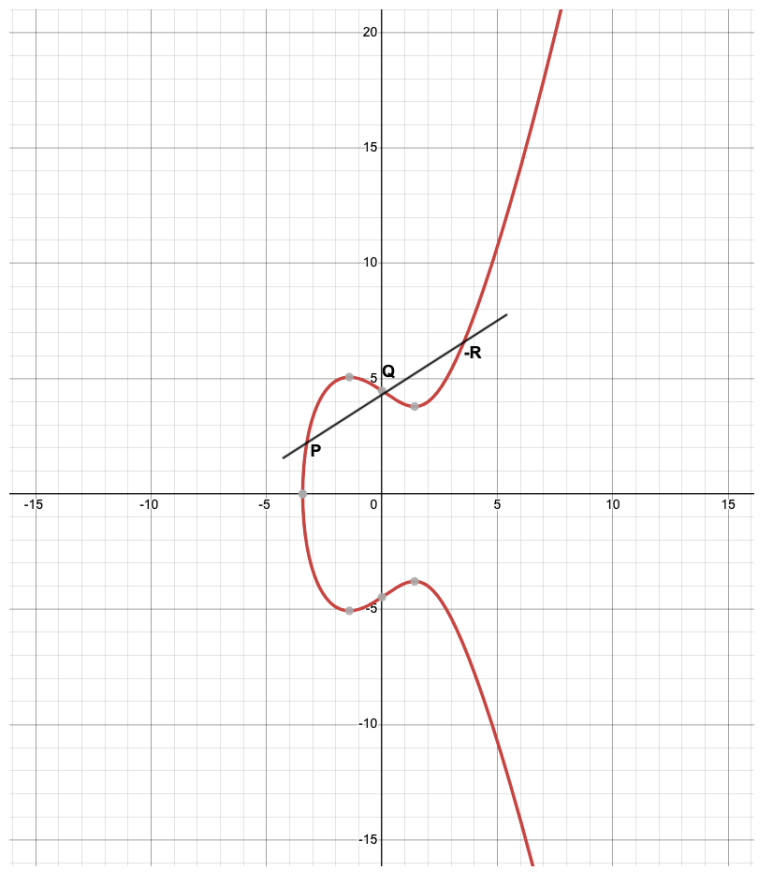
이때 -R의 X 축으로 대칭된 점을 R이라고 합니다.
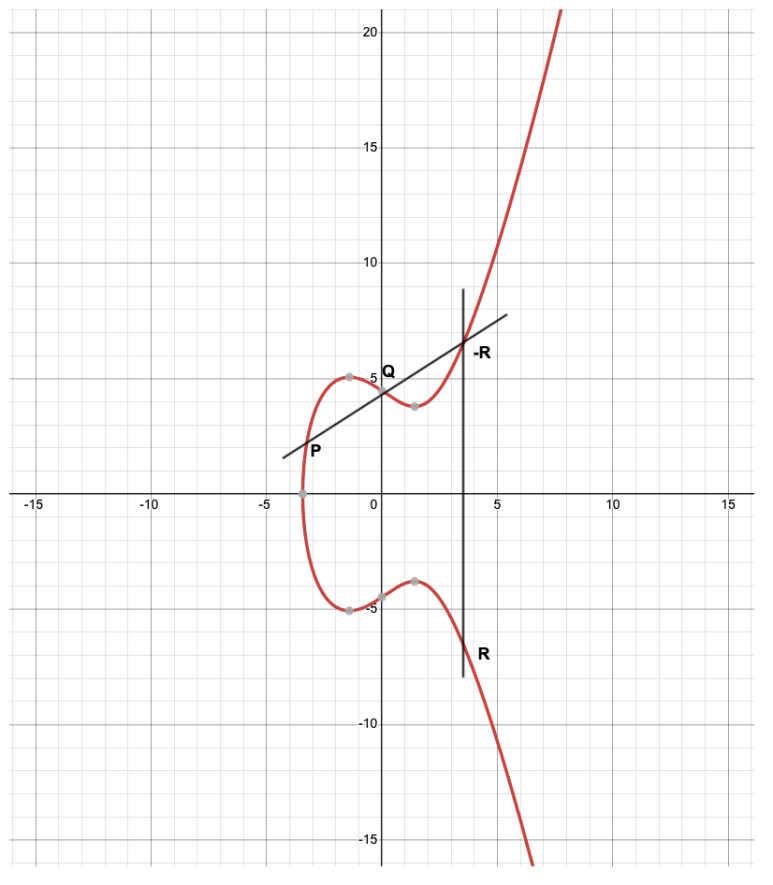
해당 점의 좌표를 ECC에서 덧셈 연산으로 표현하면 P + Q = R이라고 정의합니다.
이를 이용하여 곱셈 연산을 덧셈 연산으로 표현할 수 있습니다.
ECC는 덧셈 연산만 가능하다는 점을 꼭 기억해야 합니다.
곱셈은 덧셈의 연속이기 때문에 덧셈으로 바꿔서 해석이 가능합니다.
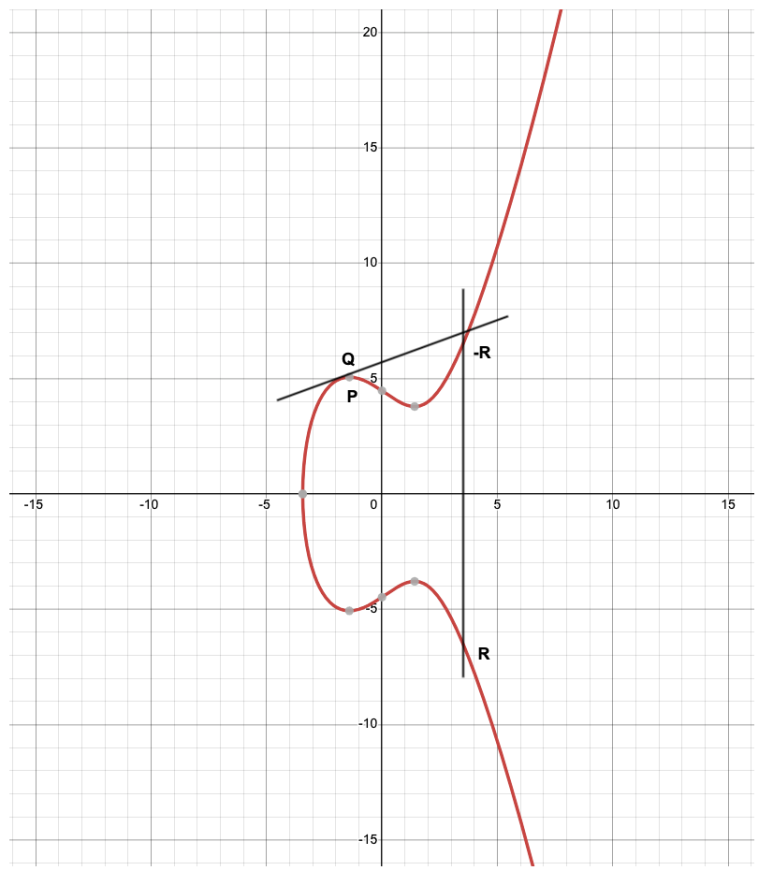
P와 Q를 두 점이 아닌 한 점으로 표현해도 동일하게 P + Q = R을 성립합니다.
P와 Q는 같기 때문에 P + Q는 P + P로 표현가능합니다.
P + P = R이 됩니다. 이는 2P = R이 됩니다. 해당 그래프에서 R은 2P가 됩니다.
그렇다면 3P는 어떻게 연산이 가능할까요? 바로 앞의 그래프에서 점 P와 점 R(2P)를 지나는 직선을 그립니다. 그리고 만나는 교점을 X축으로 대칭한 위치가 3P가 됩니다.
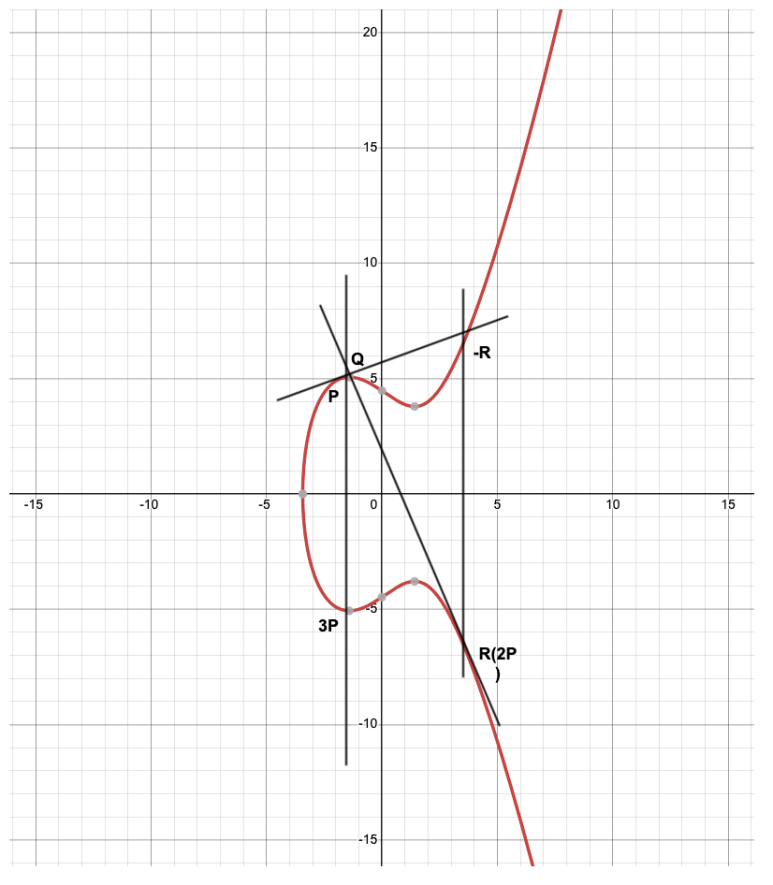
여기서 핵심은 곱셈은 덧셈의 연속으로 풀 수 있다는 점일 인지하도록 합니다.
이를 수식으로 풀면 다음과 같습니다.
P(x1, y1), Q(x2, y2)가 E 상에 존재할 때 R(x3, y3) = P(x1, y1) + Q(x2, y2)가 된다.
☞ P != Q일때(addition)
☞ P == Q일 때(Doubling)
· 모듈러(나머지) 연산
모듈러 연산은 나머지연산입니다. 연산자는 mod라고 표기합니다. 코드레벨에선 %으로 대부분 표현합니다.
10 % 3 = 1
10 mod 3 = 1만약 음수에 대한 모듈러 연산을 어떻게 해야할까요?
모듈러 연산의 특징 중 하나가 피연산자의 값을 주기로 같은 결과값을 가지는 주기성을 띕니다.
-5 mod 3은 다음과 같이 변환가능합니다.
(-5 + 3) mod 3 => -2 mod 3
-5 mod 3 = -2 mod 3 이 두식의 값은 같습니다.
(-2 + 3) mod 3 = 1 mod 3 = 1
· 갈루아 필드에서 타원 곡선(Elliptic Curves Over GF(p))
갈루아 필드는 유한체를 의미합니다.
유한한 좌표를 가지는 공간을 의미하며 이는 modular 연산을 이용합니다. mod p를 수행합니다. p는 소수로 정의합니다.
갈루아 필드는 다음과 같이 정의할 수 있습니다.
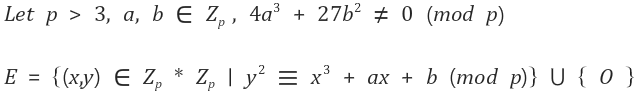
다음은 갈루아 필드의 예입니다.
$$y^2=x^3+x\ over\ {Z}_{23}\ (p=23)$$
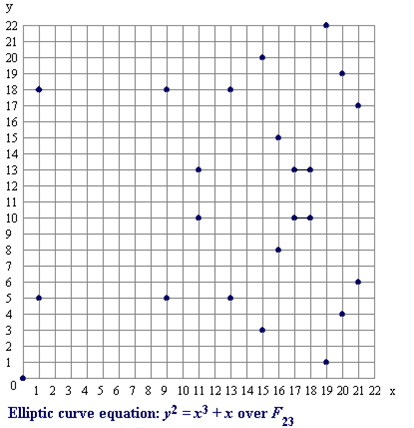
만약 x가 9라면, (9^3 + 9) mod 23 = 2가 됩니다. 이는 (5 * 5) mod 9 = 2로 표현이 가능하며 y는 5가 됩니다. 즉 x가 9일 때 y는 5가 나옵니다.
여기서 p가 커진다면 y는 쉽게 찾기 힘듭니다.
· privatekey, publickey
ECC는 퍼블릭키를 생성하기 위해 먼저 개인키(pk)를 랜덤하게 생성합니다.
퍼블릭키(pub) = pk * G(x0, y0) (G는 이미 알려져 있음 이를 베이스 포인트라고도 부름)
즉, 퍼블릭키는 G(x0, y0)을 pk번 더합니다.
여기서 이런 의문이 들 수 있습니다. G는 이미 공개가 되어있고 공개키는 공개가 되어있으면 개인키(pk)를 찾을 수 있는거 아닌가?하는 생각이 들 수 있는데 ECC에서 G와 공개키를 알 수 있다고 pk를 찾는건 매우 어렵습니다. 이를 ECDLP라고 하며 이러한 특징 때문에 ECC를 공개키 암호기술로 사용합니다.
한 가지 예시를 들어보겠습니다.
갈루아 필드가 다음과 같이 정의될 때, G = (2, 7)일때 2G를 계산해 보겠습니다.
먼저 2G는 G + G이므로 앞에서 P == Q(doubling) 공식을 대입하면 됩니다.
여기서 람다 결과인 13/14를 분자 분모를 각각 mod11을 수행합니다.
여기서 3^-1을 mod 11 연산을 하면 4가 나옵니다.
이제 G, 2G, 3G, 4G, ... KG(K는 임의의 양의정수)
pk(개인키) * G(베이스 포인트) = pub(공개키)
G=(2, 7), 2G = (5, 2), 3G = (8, 3)
4G = (10, 2), 5G = (3, 6), 6G = (7, 9)
7G = (7, 2), 8G = (3, 5), 9G = (10, 9)
● 이더리움의 개인키 공개키
트랜잭션을 만들기 위해선 트랜잭션을 서명할 개인키가 필요합니다.
이더리움은 개인키 - 공개키 - 주소 순서로 키와 주소를 생성합니다.
· 개인키 생성
개인키는 1 ~ n-1까지 정수 중 하나의 랜덤값 입니다. 여기서 n은 secp256k1 타원곡선에서 1.157920892373162e+77으로 정의됩니다.
secp256k1 타원 곡선 함수는 a=0, b=7로 정의되며 G=02 79BE667E F9DCBBAC 55A06295 CE870B07 029BFCDB 2DCE28D9 59F2815B 16F81798 입니다.
또한 유한군 소수값인 p는 FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE FFFFFC2F으로 정의합니다.
|
a = 0
b = 7
유한군 p값 = FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFF FFFFFFFE FFFFFC2F
G=02 79BE667E F9DCBBAC 55A06295 CE870B07 029BFCDB 2DCE28D9 59F2815B 16F81798
|
개인키는 1 ~ FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364140 까지의 범위를 가집니다. 해당 범위를 넘으면 올바르지 않은 키라고 에러가 발생합니다.
const { Wallet } = require('ethers');
async function main() {
const private = 'FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364140';
const wallet = new Wallet(private);
console.log(wallet)
}
main()
/*
Wallet {
_isSigner: true,
_signingKey: [Function (anonymous)],
_mnemonic: [Function (anonymous)],
address: '0x80C0dbf239224071c59dD8970ab9d542E3414aB2',
provider: null
}
*/const { Wallet } = require('ethers');
async function main() {
const private = 'FFFFFFFFFFFFFFFFFFFFFFFFFFFFFFFEBAAEDCE6AF48A03BBFD25E8CD0364141';
const wallet = new Wallet(private);
console.log(wallet)
}
main()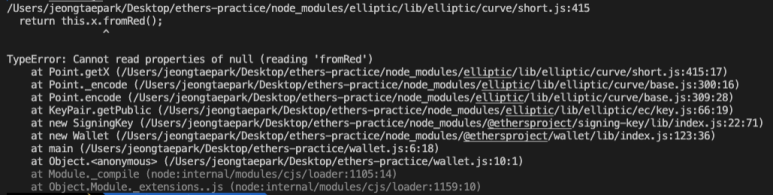
ECC는 개인키를 구한 후 공개키를 구하지만 RSA는 공개키를 구한 후 개인키를 구합니다.
· 공개키
공개키는 개인키로 생성합니다. 개인키와 이더리움에서 정한 기준점 G를 곱합니다.
공개키 = 개인키 * G
공개키는 ECC의 덧셈 연산을 통해서 연산합니다. 기준점 G를 개인키만큼 더합니다.
· 주소
주소는 공개키를 keccak-256 해싱 결과의 마지막 20바이트입니다.
● 트랜잭션 서명과 검증
이더리움은 트랜잭션 서명을 위해 ECC를 이용한 디지털 서명을 수행합니다.
이를 ECDSA라고 합니다. ECDSA는 타원 곡선 디지털 서명 알고리즘입니다. ECDSA에서 secp256k1을 이용합니다.
트랜잭션 서명을 위해 r, s, v를 트랜잭션에 포함해야 합니다.
r과 s는 서명입니다. v는 공개키를 복구하는 키 입니다. 이더리움 트랜잭션을 서명할 때 공개키를 포함하지 않고 공개키를 복구할 수 있도록 공개키 복구키인 v를 포함합니다
· 서명 r 생성
트랜잭션 서명을 위해 r을 만드는 과정은 다음과 같습니다.
개인키를 만든 것 처럼 1 ~ n-1 난수를 생성합니다. 여기서 생성된 난수를 k라고 하겠습니다.
개인키의 경우 한 번 생성되면 계속 사용하지만 서명 r은 트랜잭션을 서명할 때마다 새로 생성합니다. ECC식인 P = k * G를 통해 점 P의 좌표를 구합니다. 이때 x 좌표가 서명 r값이 됩니다.
· 서명 s 생성
s는 서명 r을 생성하기 위해 만든 난수 k를 이용합니다.
z는 트랜잭션 정보를 RLP 인코딩한 값입니다.
r은 서명 r입니다.
p는 개인키입니다.
만약, 이때 서명 s가 0이 나오면 k를 새롭게 생성하고 다시 계산합니다.
▶ (RLP 인코딩 시 포함하는 트랜잭션 정보는 다음과 같습니다.)
nonce, gasprice, startgas, to, value, data, chainID, 0, 0
EIP-155에서 simple replay attack protection을 위해 chainID를 포함하여 인코딩하는 것을 권장합니다.
EIP-155: Simple replay attack protection
eips.ethereum.org
· 공개키 복구키 v 생성
이더리움에서는 트랜잭션에 공개키를 추가하지 않습니다. v라는 값을 이용하여 공개키를 복구 할 수 있도록 합니다.
EIP-155에서 v는 다음과 같이 정의합니다.
v = CHAIN_ID * 2 + 35 또는 v = CHAIN_ID * 2 + 36
즉, 메인넷 기준으로 37 또는 38이 나옵니다. 또한 0 + 27 또는 1 + 27을 사용하기도 합니다.
· 트랜잭션 전송
서명 s, 서명 r, 복구키 v를 트랜잭션에 포함한 후 RLP 인코딩하여 전송합니다.
· 트랜잭션 검증
트랜잭션 검증은 별도의 식이 있습니다.
트랜잭션 검증 식 = U1 * G + U2 * public key
w = s^-1 mod n (s = s서명)
U1 = z * w mod n (z = 트랜잭션 RLP 인코딩)
U2 = r * w mod n (r = r서명)
U1과 U2는 서명 s와 서명 r을 이용하여 알 수 있습니다. public key는 복구키인 v를 이용하여 복구할 수 있습니다. 복구키 v는 서명 r과 서명 s값만 가지고 공개키를 추출할 수 있도록 합니다.
solidity에서는 ecrecover() 함수를 제공합니다.
트랜잭션 검증식은 타원곡선의 연산으로 타원곡선 위의 점이 나오게 되며 해당점의 x 좌표값과 트랜잭션에 포함된 서명 r값이 같으면 해당 트랜잭션을 유효하다고 판단합니다.
참고자료:
https://eips.ethereum.org/EIPS/eip-155
https://steemit.com/kr/@icoreport/key-2-ecc
그래프 생성도구:
